Model 1: A Simple Dengue Model
The following is my rendition of a 2018 Kong et al. model for the 2014 dengue (DENV) outbreak in Guangzhou, China using EpiModel.
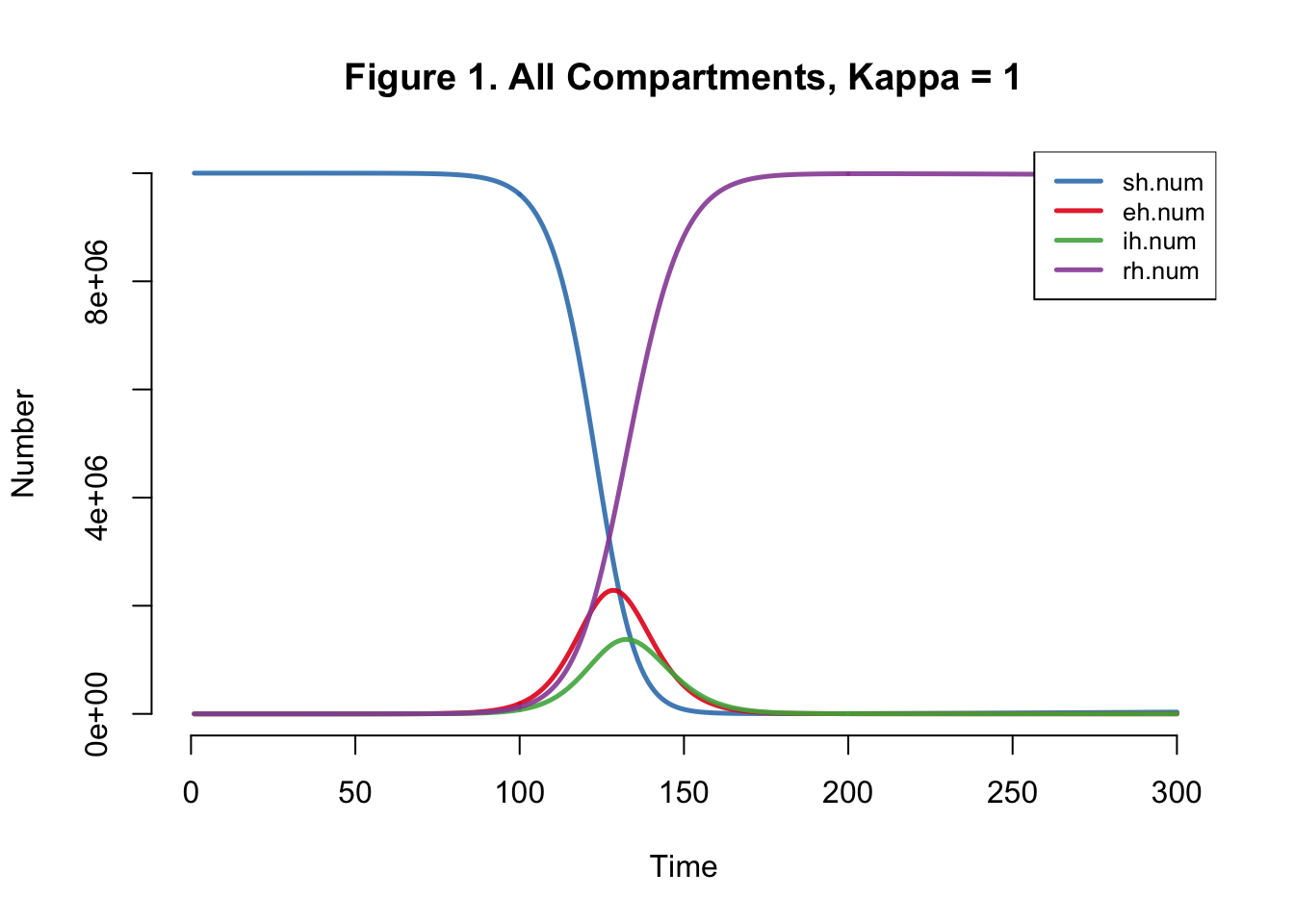
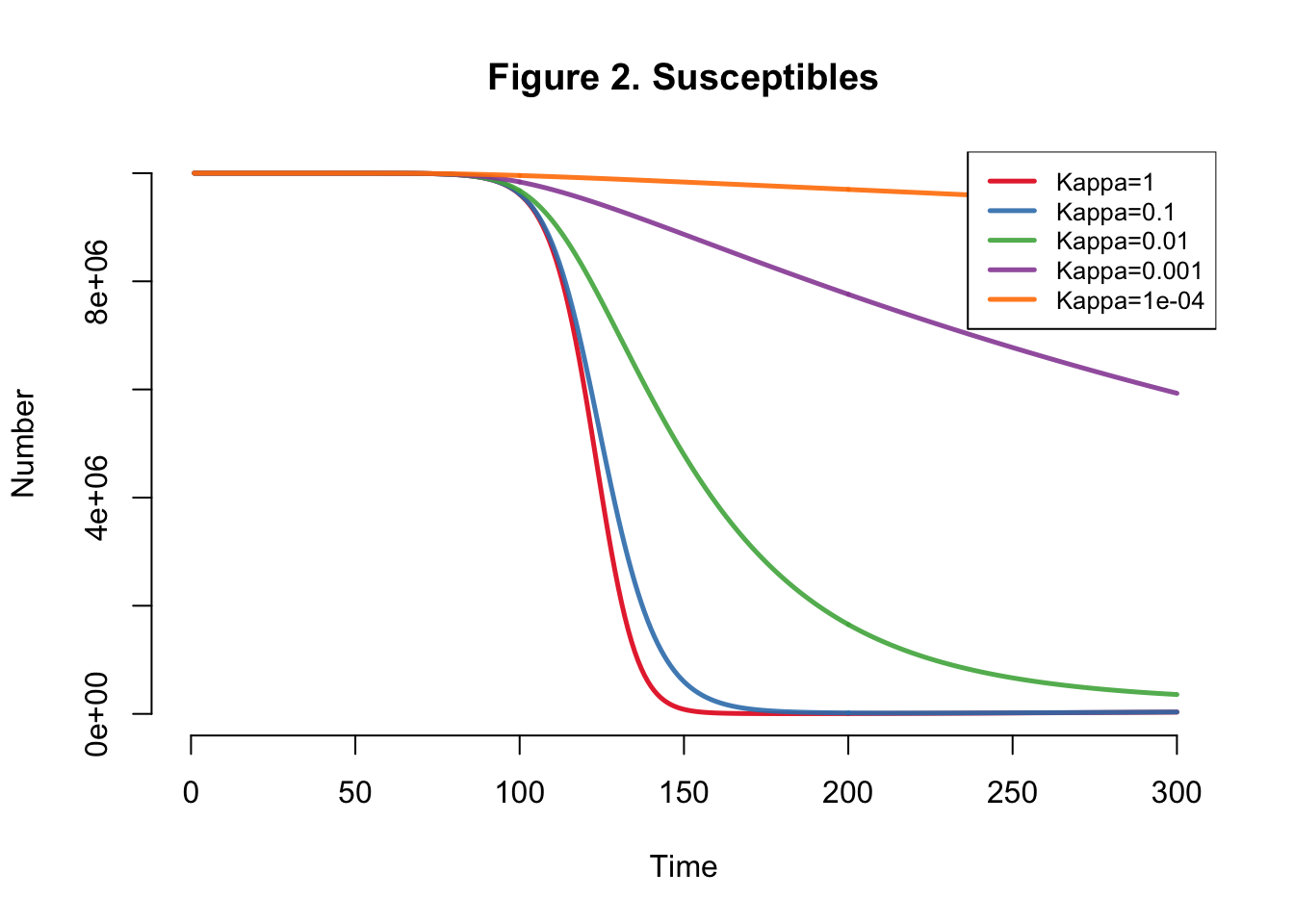
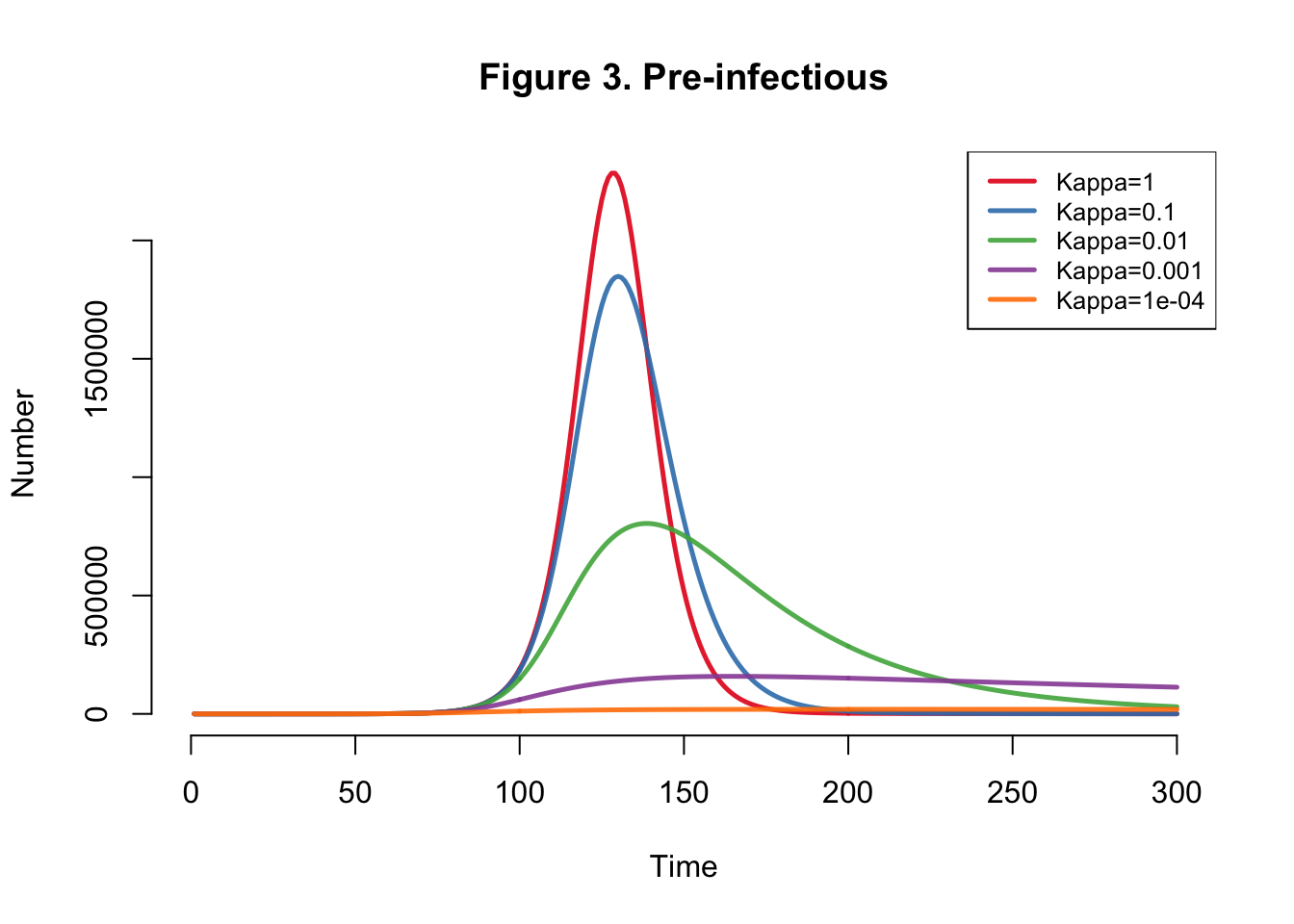
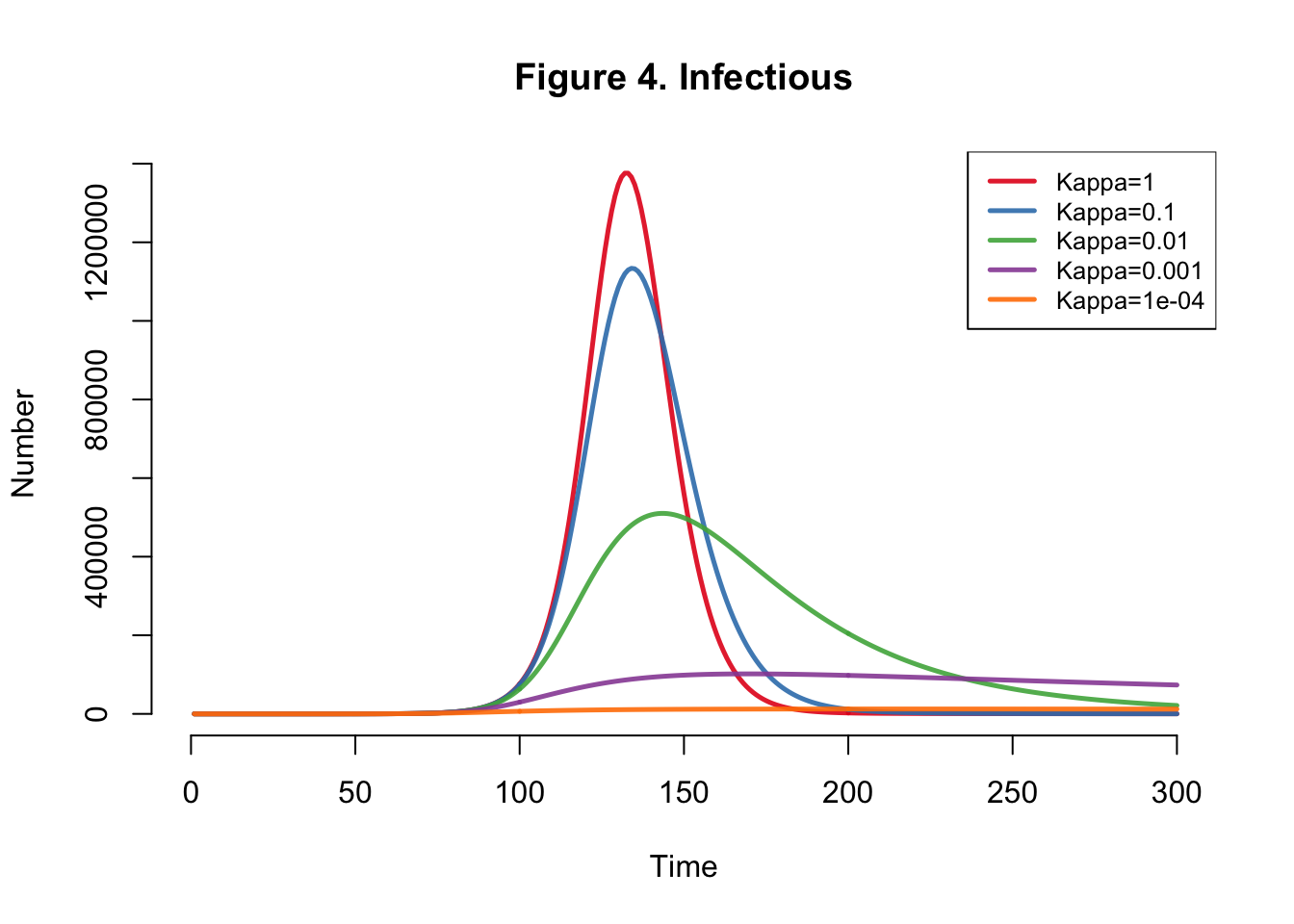
I developed the SEIR-SEI model described by Kong et al., where SEIR respresents the human compartments and SEI represents the vector compartments. The total infections for this outbreak depending on transmission heterogeneity (kappa) ranges between 558,000 and 10 million (Table 1). This illustrates the importance of accounting for dispersion (i.e. superspreading, clustering, heterogeneity, etc.) in all transmission models. The Kong et al. Figure 6 matches Figure 4 below.
In a subsequent post, I’ll develop the extended model in this paper and try to fit to their data.
Full code is on Github.
Reference: Kong L, Wang J, Li Z, et al. Modeling the Heterogeneity of Dengue Transmission in a City. Int J Environ Res Public Health. 2018;15(6):1128. Published 2018 May 31. doi:10.3390/ijerph15061128
Model
denv <-function(t, t0, parms) {
with(as.list(c(t0, parms)), {
numH <- sh.num + eh.num + ih.num + rh.num
numV <- sv.num + ev.num + iv.num
lambdaH <- log(1 + ((alpha*rhoV*iv.num)/(kappa*numH)))
lambdaV <- log(1 + ((alpha*rhoH*ih.num)/(kappa*numH)))
dSh <- (muH*numH) - (kappa*lambdaH*sh.num) - (muH*sh.num)
dEh <- (kappa*lambdaH*sh.num) - ((deltaH + muH)*eh.num)
dIh <- (deltaH*eh.num) - ((gammaH + muH)*ih.num)
dRh <- (gammaH*ih.num) - (muH*rh.num)
dSv <- (muV*numV) - (kappa*lambdaV*sv.num) - (muV*sv.num)
dEv <- (kappa*lambdaV*sv.num) - ((deltaV + muV)*ev.num)
dIv <- (deltaV*ev.num) - (muV*iv.num)
list(c(dSh,
dEh,
dIh,
dRh,
dSv,
dEv,
dIv,
se.flow <- (kappa*lambdaH*sh.num),
ei.flow <- (deltaH*eh.num),
ir.flow<- (gammaH*ih.num)
))
})
}Plots
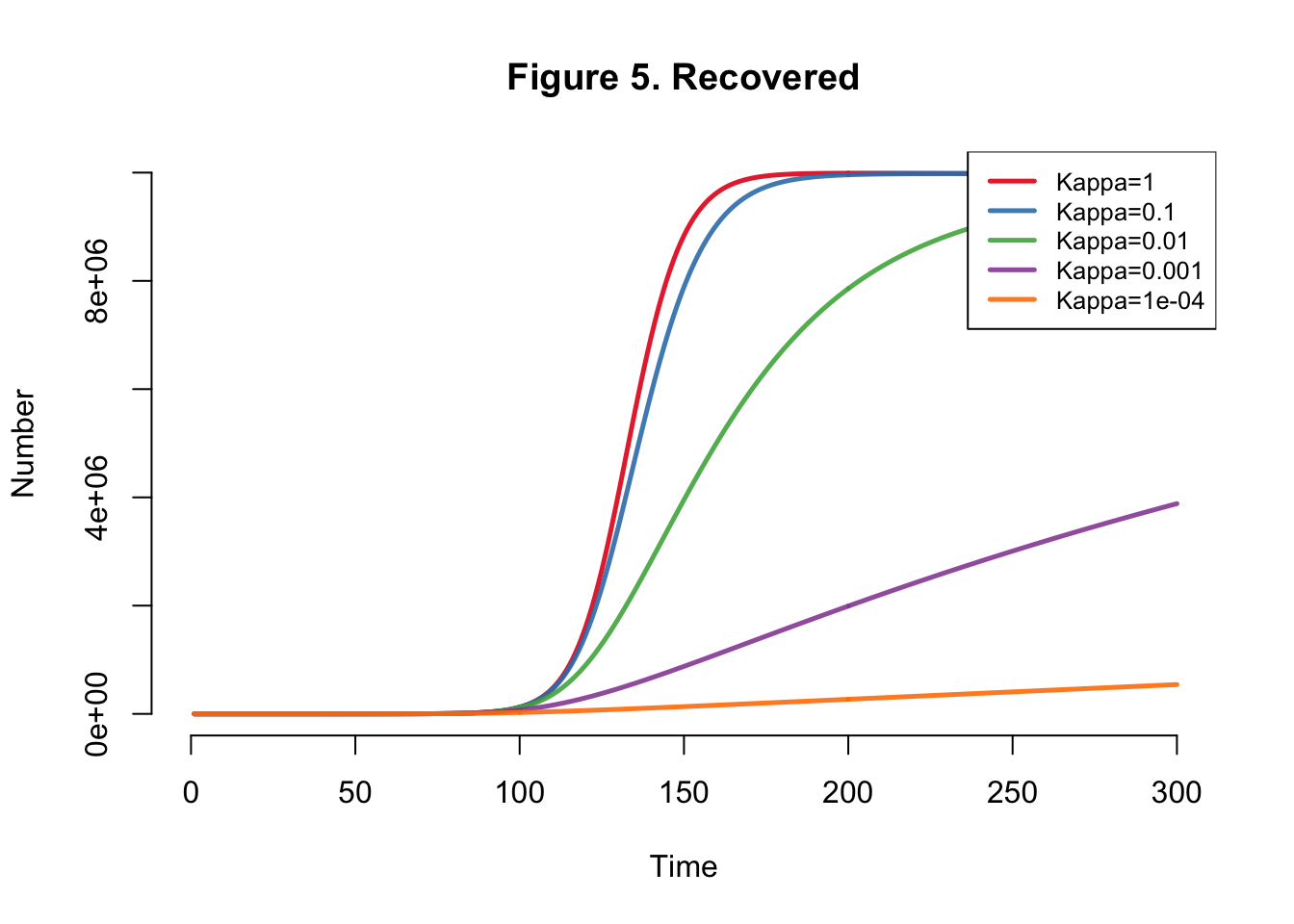
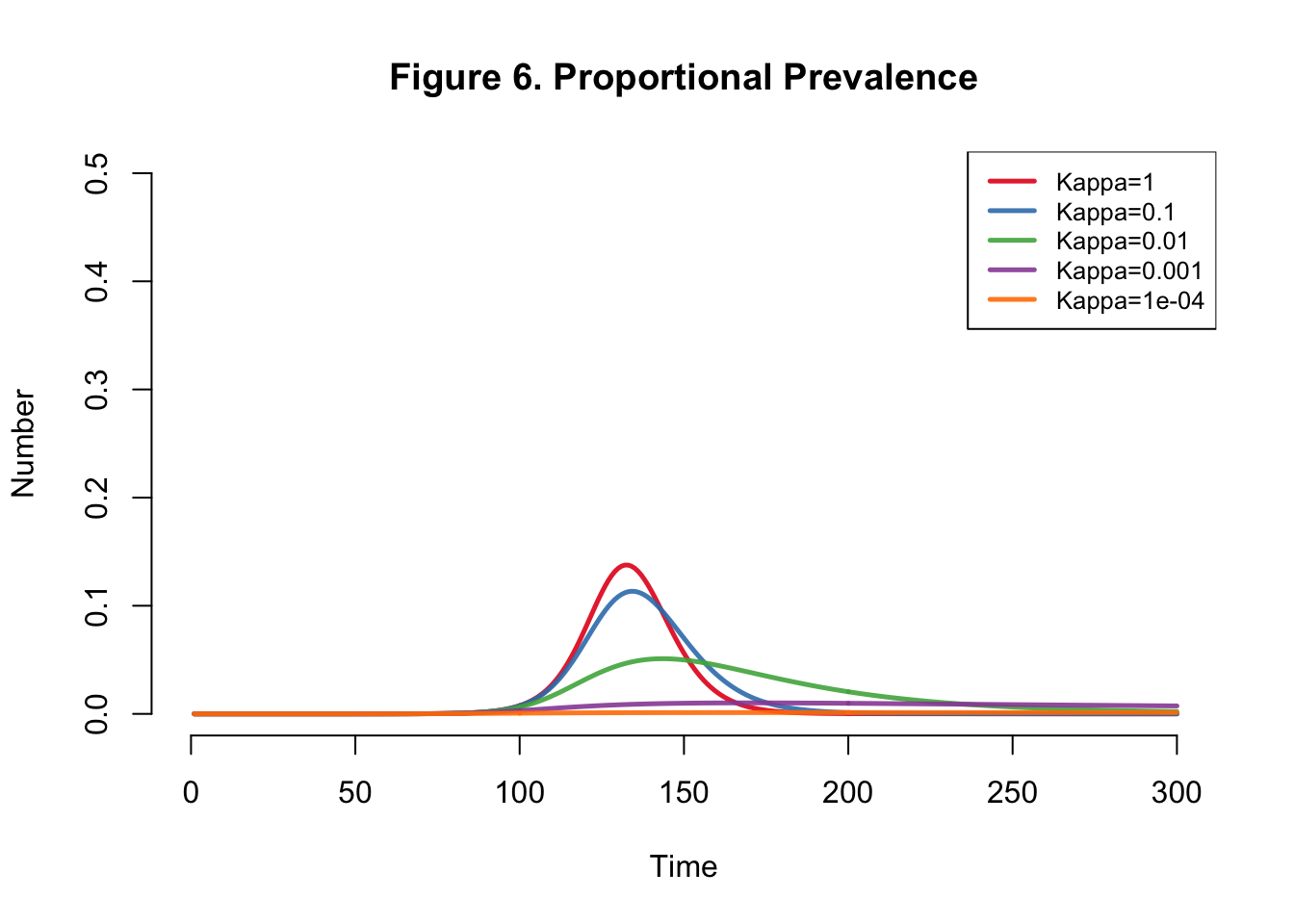
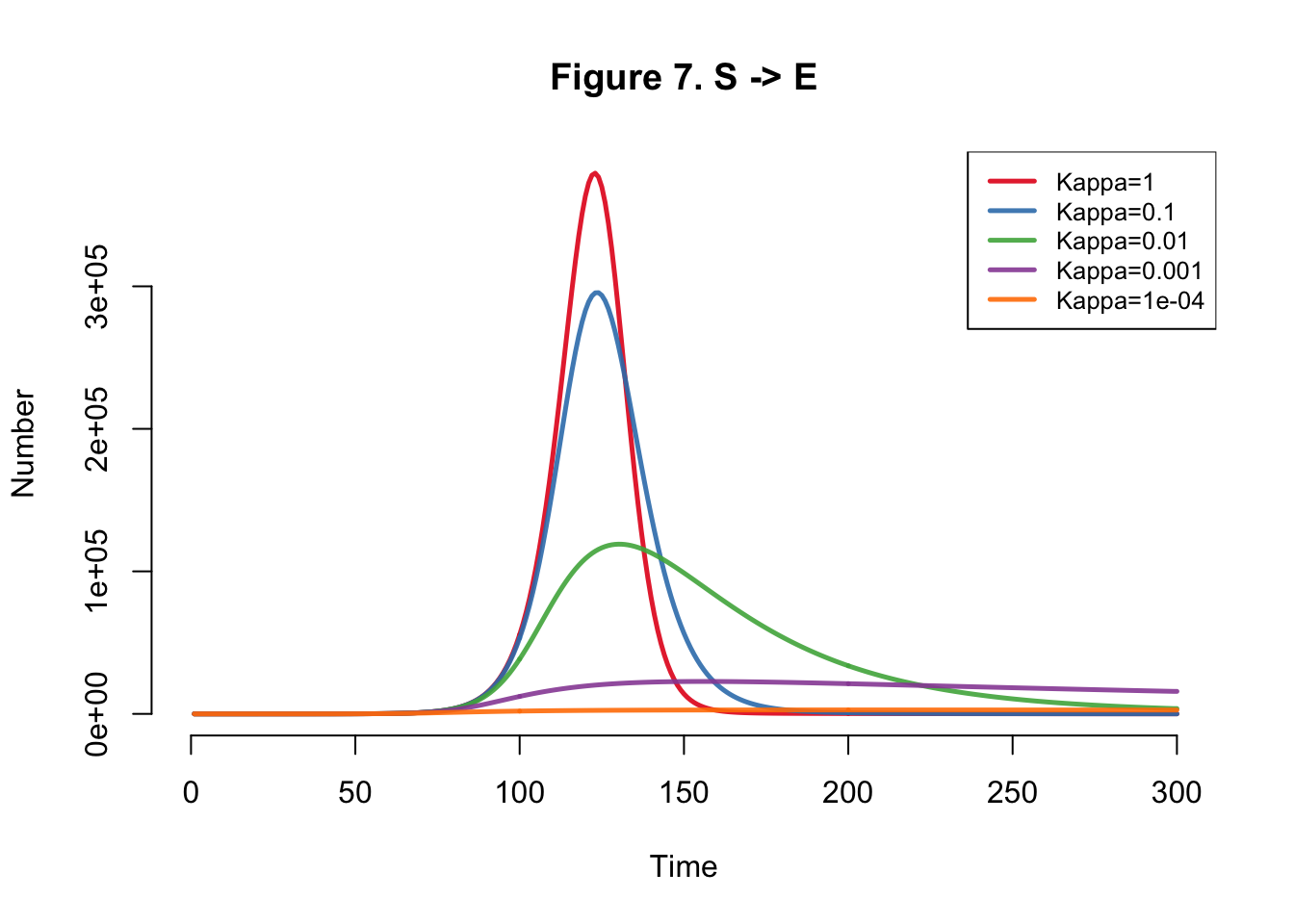
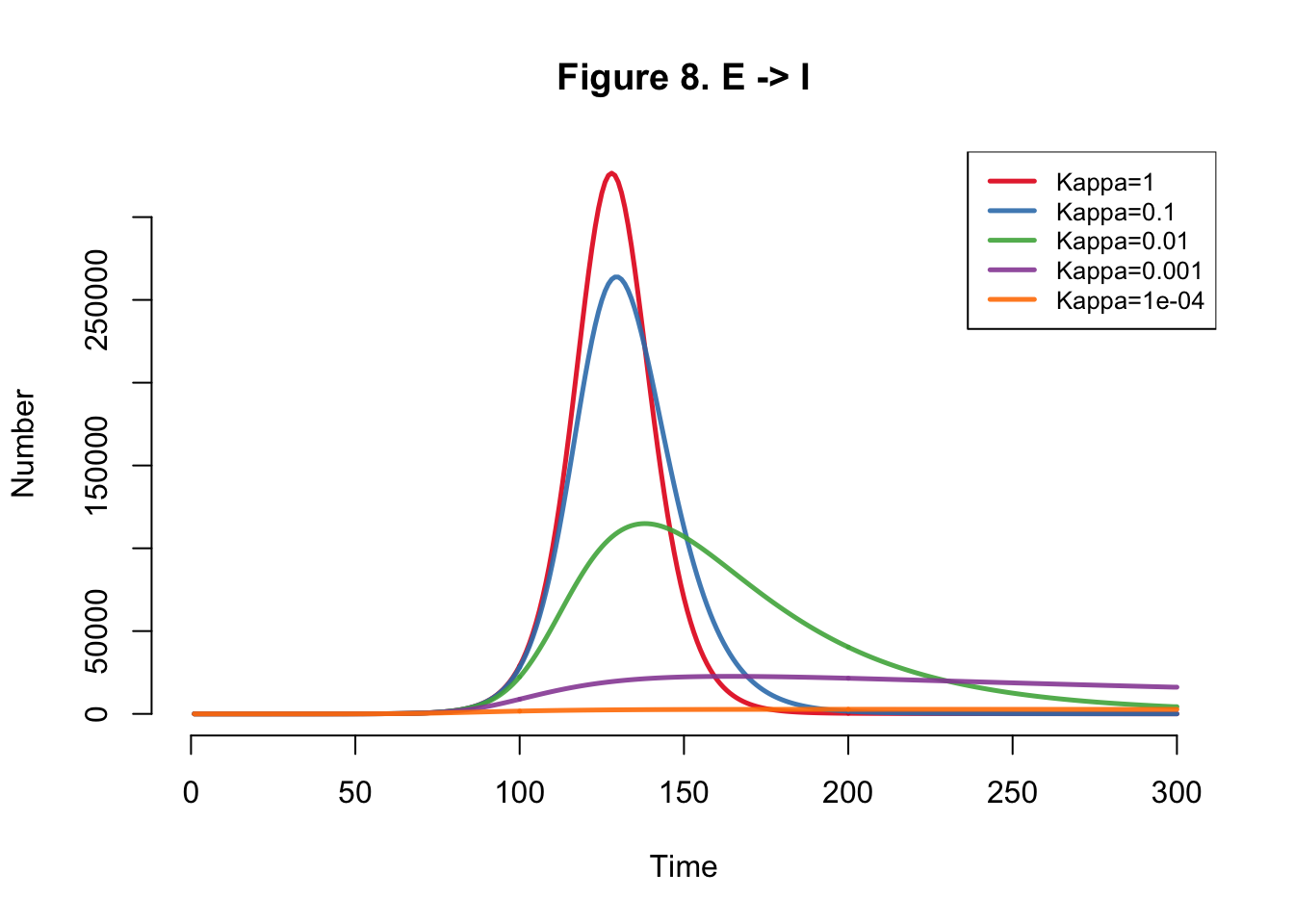
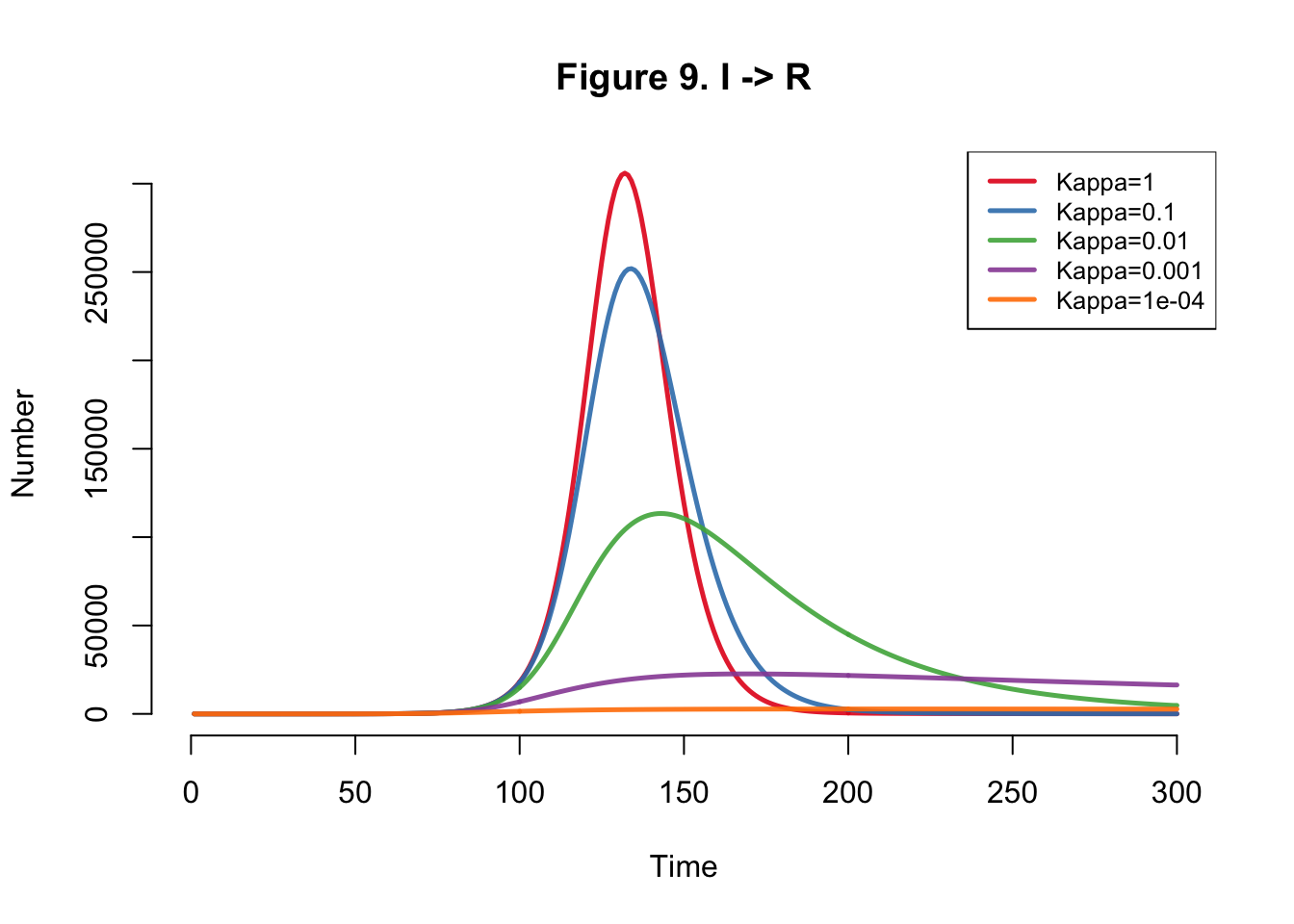
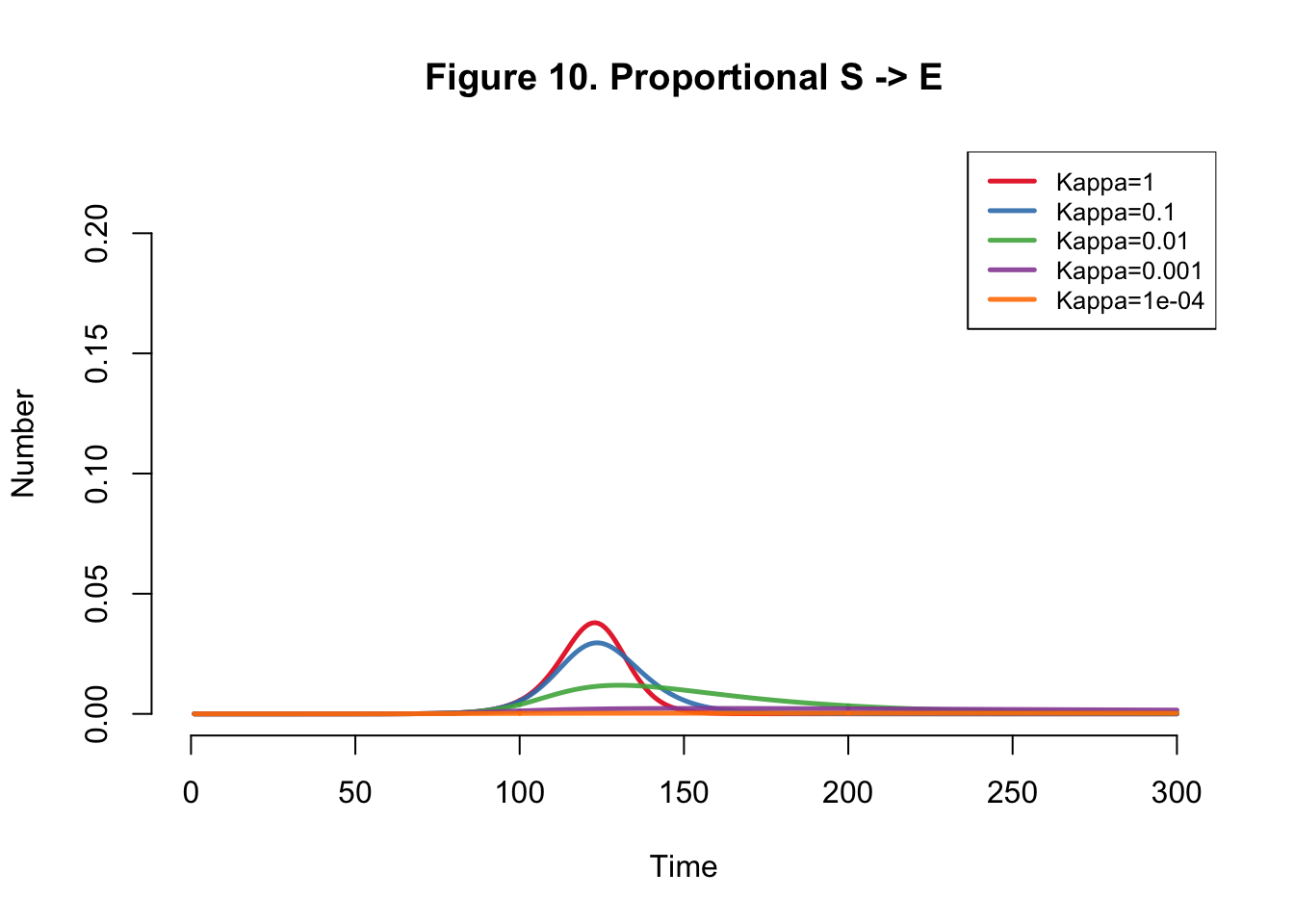
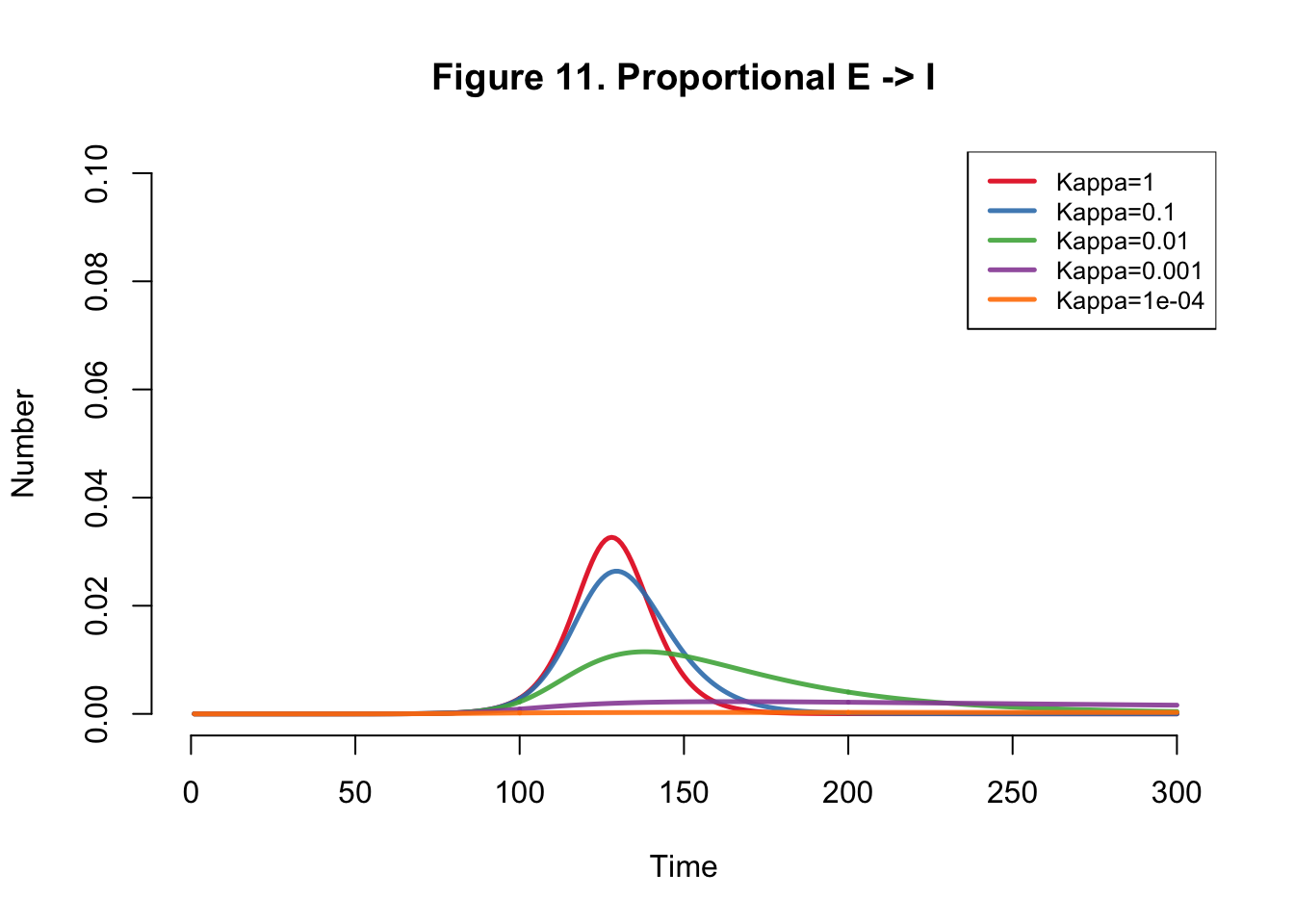
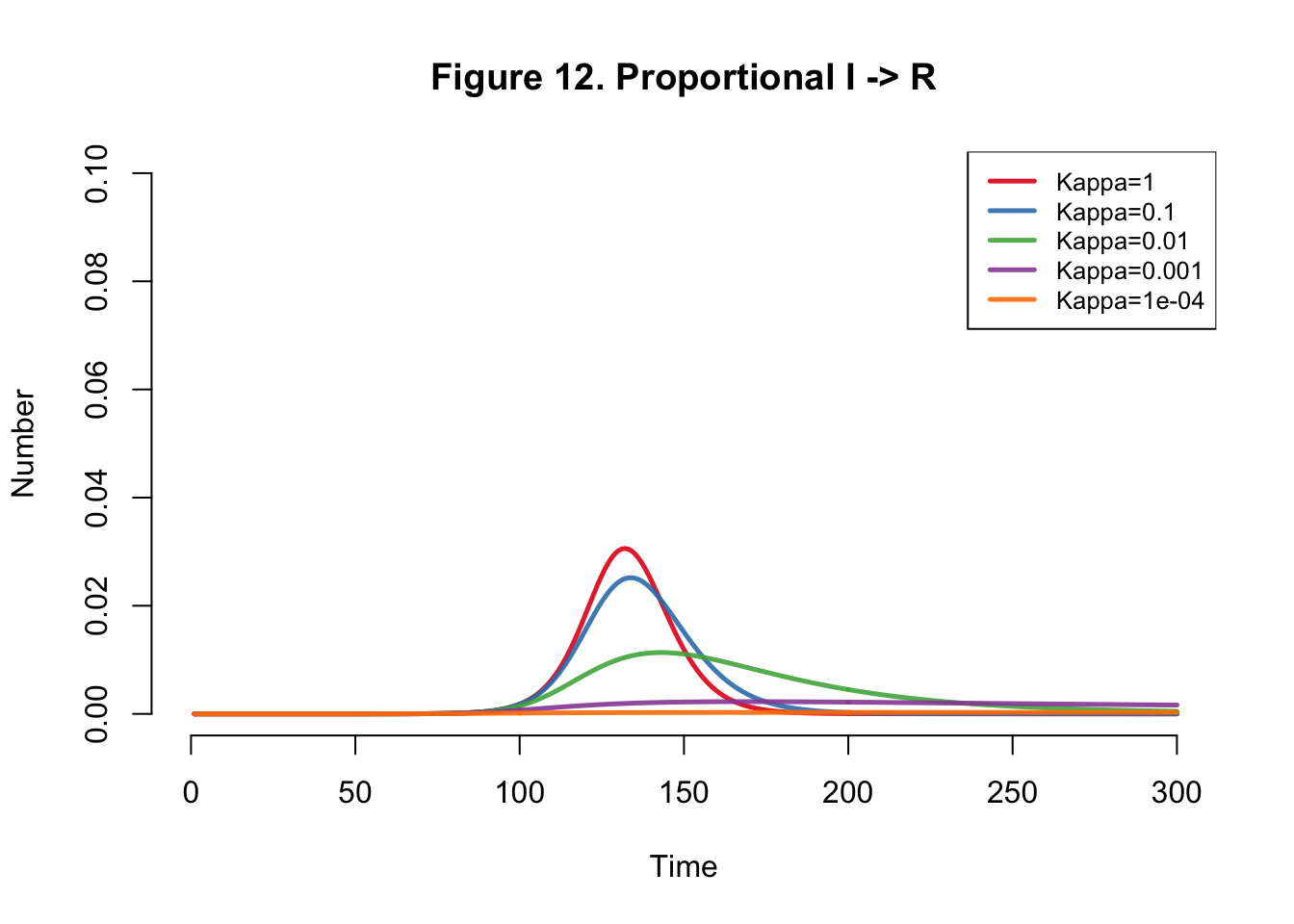
| Kappa | Total |
|---|---|
| 1e+00 | 10,029,378 |
| 1e-01 | 10,026,356 |
| 1e-02 | 9,665,063 |
| 1e-03 | 3,988,658 |
| 1e-04 | 558,594 |